转载 :详解圈复杂度
圈复杂度(Cyclomatic complexity,简写CC)也称为条件复杂度,是一种代码复杂度的衡量标准。由托马斯·J·麦凯布(Thomas J. McCabe, Sr.)于1976年提出,用来表示程序的复杂度,其符号为VG或是M。它可以用来衡量一个模块判定结构的复杂程度,数量上表现为独立现行路径条数,也可理解为覆盖所有的可能情况最少使用的测试用例数。圈复杂度大说明程序代码的判断逻辑复杂,可能质量低且难于测试和维护。程序的可能错误和高的圈复杂度有着很大关系。
圈复杂度的计算方法很简单,计算公式为:
V(G) = E - N + 2
其中,e表示控制流图中边的数量,n表示控制流图中节点的数量。
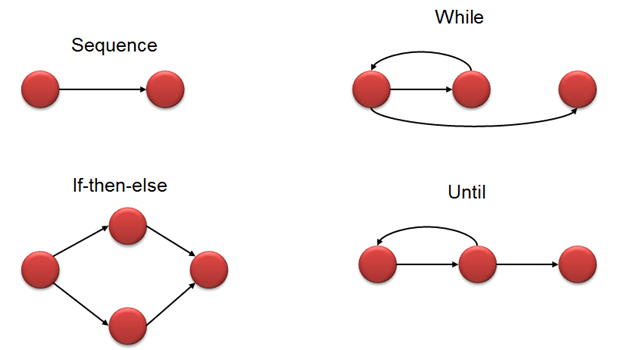
几个节点通过边连接。下面是典型的控制流程,如if-else,While,until和正常的流程顺序:
其实,圈复杂度的计算还有更直观的方法,因为圈复杂度所反映的是“判定条件”的数量,所以圈复杂度实际上就是等于判定节点的数量再加上1,也即控制流图的区域数,对应的计算公式为:
V (G) = P + 1
其中P为判定节点数,判定节点举例:
if语句
while语句
for语句
case语句
catch语句
and和or布尔操作
?:三元运算符
对于多分支的CASE结构或IF-ELSEIF-ELSE结构,统计判定节点的个数时需要特别注意一点,要求必须统计全部实际的判定节点数,也即每个ELSEIF语句,以及每个CASE语句,都应该算为一个判定节点。
判定节点在模块的控制流图中很容易被识别出来,所以,针对程序的控制流图计算圈复杂度V(G)时,一般采用点边计算法,也即V(G)=e-n+2;而针对模块的控制流图时,可以直接使用统计判定节点数,这样更为简单。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 void sort (int * A) int i=0 ; int n=4 ; int j = 0 ; while (i < n-1 ) { j = i +1 while (j < n) { if (A[i] < A[j]) swap(A[i], A[j]); } i = i + 1 } }
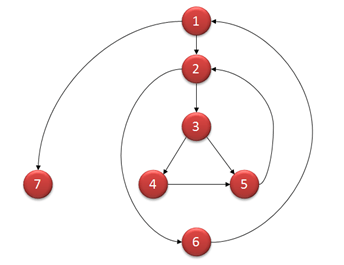
使用点边计算法绘出控制流图:
其圈复杂度为:V(G) = 9 - 7 + 2 = 4
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 U32 find (string match) { for (auto var : list ) { if (var == match && from != INVALID_U32) return INVALID_U32; } if (session == getName() && key == getKey ()) { for (auto & kv : Map) { if (kv.second == last && match == kv.first) { return last; } } } auto var = Map.find (match); if (var != Map.end ()&& (from != var->second)) return var->second; for (auto var: Map) { if ((var.first, match) && from != var.second) { return var.second; } } return INVALID_U32; };
其圈复杂度为:V(G) = 1(for) + 2(if) + 2(if) + 1(for) + 2(if) + 2(if) + 1(for) + 2(if) + 1= 14
在缺陷成为缺陷之前捕获它们。
一般来说圈复杂度大于10的方法存在很大的出错风险。圈复杂度和缺陷个数有高度的正相关:圈复杂度最高的模块和方法,其缺陷个数也可能最多。
此外,它还为测试设计提供很好的参考。一个好的用例设计经验是:**创建数量与被测代码圈复杂度值相等的测试用例,**以此提升用例对代码的分支覆盖率。
TDD(测试驱动的开发,test-driven development)和低CC 值之间存在着紧密联系。在编写测试时,开发人员会考虑代码的可测试性,倾向于编写简单的代码,因为复杂的代码难以测试。因此TDD的“代码、测试、代码、测试” 循环将导致频繁重构,驱使非复杂代码的开发。
对于遗留代码的维护或重构,测量圈复杂度特别有价值。一般使用圈复杂度作为提升代码质量的切入点。
在持续集成环境中,可以基于时间变化维度来评估模块或函数的复杂度和增长值。如果CC 值在不断增长,那么应该开展两项活动:
确保相关测试的有效性,减少故障风险。
评估重构必要性和具体方式,以降低出现代码维护问题的可能性。
圈复杂度
代码状况
可测性
维护成本
1-10
清晰、结构化
高
低
10-20
复杂
中
中
20-30
非常复杂
低
高
>30
不可读
不可测
非常高
有一段代码可以被组织在一起并独立出来:
1 2 3 4 5 6 7 8 9 10 11 12 void Example (int val) if ( val > MAX_VAL) { val = MAX_VAL; } for ( int i = 0 ; i < val; i++) { doSomething(i); } }
将这段代码放进一个独立函数中,并让函数名称解释该函数的用途:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 int getValidVal (int val) if ( val > MAX_VAL) { return MAX_VAL; } return val; } void doSomethings (int val) for ( int i = 0 ; i < val; i++) { doSomething(i); } } void Example (int val) doSomethings(getValidVal(val)); }
最后还要重新审视函数内容是否在统一层次上。
把某个算法替换为另一个更清晰的算法:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 string foundPerson (const vector <string >& peoples) for (auto & people : peoples) { if (people == "Don" ){ return "Don" ; } if (people == "John" ){ return "John" ; } if (people == "Kent" ){ return "Kent" ; } } return "" ; }
将函数实现替换为另一个算法:
1 2 3 4 5 6 7 8 9 10 11 12 13 string foundPerson (const vector <string >& people) std ::map <string ,string >candidates{ { "Don" , "Don" }, { "John" , "John" }, { "Kent" , "Kent" }, }; for (auto & people : peoples) { auto & it = candidates.find (people); if (it != candidates.end ()) return it->second; } }
所谓的表驱动。
在代码中可能存在条件表达如下:
1 2 3 4 5 6 7 8 if ((condition1() && condition2()) || !condition1()){ return true ; } else { return false ; }
应用逆向表达调换表达顺序后效果如下:
1 2 3 4 5 6 if (condition1() && !condition2()){ return false ; } return true ;
在代码中存在复杂的条件表达:
1 2 3 4 if (date.before (SUMMER_START) || date.after(SUMMER_END)) charge = quantity * _winterRate + _winterServiceCharge; else charge = quantity * _summerRate;
从if、then、else三个段落中分别提炼出独立函数:
1 2 3 4 if (notSummer(date)) charge = winterCharge(quantity); else charge = summerCharge (quantity);
一系列条件判断,都得到相同结果:
1 2 3 4 5 6 7 double disabilityAmount () if (_seniority < 2 ) return 0 ; if (_monthsDisabled > 12 ) return 0 ; if (_isPartTime) return 0 ; ......
将这些判断合并为一个条件式,并将这个条件式提炼成为一个独立函数:
1 2 3 4 5 double disabilityAmount () if (isNotEligableForDisability()) return 0 ; ......
在代码逻辑中,有时候会使用bool类型作为逻辑控制标记:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 void checkSecurity (vector <string >& peoples) bool found = false ; for (auto & people : peoples) { if (! found) { if (people == "Don" ){ sendAlert(); found = true ; } if (people == "John" ){ sendAlert(); found = true ; } } } }
使用break和return取代控制标记:
1 2 3 4 5 6 7 8 9 10 void checkSecurity (vector <string >& peoples) for (auto & people : peoples) { if (people == "Don" || people == "John" ) { sendAlert(); break ; } } }
条件式根据对象类型的不同而选择不同的行为:
1 2 3 4 5 6 7 8 9 10 11 12 double getSpeed () switch (_type) { case EUROPEAN: return getBaseSpeed(); case AFRICAN: return getBaseSpeed() - getLoadFactor() *_numberOfCoconuts; case NORWEGIAN_BLUE: return (_isNailed) ? 0 : getBaseSpeed(_voltage); } throw new RuntimeException ("Should be unreachable" ); }
将整个条件式的每个分支放进一个子类的重载方法中,然后将原始函数声明为抽象方法:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 class Bird { public : virtual double getSpeed () 0 ; protected : double getBaseSpeed () } class EuropeanBird { public : double getSpeed () { return getBaseSpeed(); } } class AfricanBird { public : double getSpeed () { return getBaseSpeed() - getLoadFactor() *_numberOfCoconuts; } private : double getLoadFactor () double _numberOfCoconuts; } class NorwegianBlueBird { public : double getSpeed () { return (_isNailed) ? 0 : getBaseSpeed(_voltage); }; private : bool _isNailed; }
某个函数既返回对象状态值,又修改对象状态:
1 2 3 4 class Customer { int getTotalOutstandingAndSetReadyForSummaries (int number) }
建立两个不同的函数,其中一个负责查询,另一个负责修改:
1 2 3 4 5 class Customer { int getTotalOutstanding () void SetReadyForSummaries (int number) }
若干函数做了类似的工作,但在函数本体中却 包含了不同的值:
1 2 3 4 5 6 7 8 9 10 11 12 13 Dollars baseCharge () { double result = Math.min (lastUsage(),100 ) * 0.03 ; if (lastUsage() > 100 ) { result += (Math.min (lastUsage(),200 ) - 100 ) * 0.05 ; } if (lastUsage() > 200 ) { result += (lastUsage() - 200 ) * 0.07 ; } return new Dollars (result); }
建立单一函数,以参数表达那些不同的值:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Dollars baseCharge () double result = usageInRange(0 , 100 ) * 0.03 ; result += usageInRange (100 ,200 ) * 0.05 ; result += usageInRange (200 , Integer.MAX_VALUE) * 0.07 ; return new Dollars (result); } int usageInRange (int start, int end ) if (lastUsage() > start) return Math.min (lastUsage(),end ) -start; return 0 ; }
函数实现完全取决于参数值而采取不同反应:
1 2 3 4 5 6 7 8 void setValue (string name, int value) if (name == "height" ) _height = value; else if (name == "width" ) _width = value; Assert.shouldNeverReachHere(); }
针对该参数的每一个可能值,建立一个独立函数:
1 2 3 4 5 6 7 8 void setHeight (int arg) _height = arg; } void setWidth (int arg) _width = arg; }
还是以之前统计CC 值的例子:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 U32 find (string match) { for (auto var : List) { if (var == match && from != INVALID_U32) return INVALID_U32; } if (session == getName() && key == getKey ()) { for (auto & kv : Map) { if (kv.second == last && match == kv.first) { return last; } } } auto var = Map.find (match); if (var != Map.end ()&& (from != var->second)) return var->second; for (auto var: Map) { if ((var.first, match) && from != var.second) { return var.second; } } return INVALID_U32; };
综合运用降低CC值的技巧后:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 namespace { struct Matcher { Matcher(string name, string key); U32 find () ; private : bool except () U32 matchStep1 () ; U32 matchStep2 () ; U32 matchStep3 () ; bool isTheSameMatch () string match; U32 from; }; Matcher::Matcher(string name, string key): match(name + key) { from = GetFrom(); } U32 Matcher::find () { if (except()) return INVALID_U32; auto result = matchStep1(); if (result != INVALID_U32) return result; result = matchStep2(); if (result != INVALID_U32) return result; return matchStep3(); } bool Matcher::except () { for (auto var : List) { if (var == match && from != INVALID_U32) return true ; } return false ; } U32 Matcher::matchStep1 () { if (!isTheSameMatch()) { return INVALID_U32; } for (auto & kv : Map) { if ( last == kv.second && match == kv.first) { return last; } } return INVALID_U32; } bool Matcher::isTheSameMatch () { return match == getName() + getKey (); } U32 Matcher::matchStep2 () { auto var = Map.find (match); if (var != Map.end ()&& (from != var->second)) { return var->second; } return INVALID_U32; } U32 Matcher::matchStep3 () { for (auto var: Map) { if (keyMatch(var.first, match) && from != var.second) { return var.second; } } return INVALID_U32; } } U32 find (string match) Matcher matcher; return matcher.find (match); }
该例子将匹配算法都封装到Matcher类中,并将原有逻辑通过提炼函数(技巧1)和合并条件(技巧6)将匹配逻辑抽象成能力查询、粘滞、精确匹配及模糊匹配四个步骤,这样将循环和条件分支封入小函数中,从而降低接口函数(findPno)的圈复杂度,函数职责也更加单一和清晰。整体圈复杂度从单个函数的14降到多个函数最高的5。
在实际项目中为了调试方便,经常会把消息号对应的名称打印出来:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 string getMessageName (Message msg) switch (msg) { case MSG_1: return "MSG_1" ; case MSG_2: return "MSG_2" ; case MSG_3: return "MSG_3" ; case MSG_4: return "MSG_4" ; case MSG_5: return "MSG_5" ; case MSG_6: return "MSG_6" ; case MSG_7: return "MSG_7" ; case MSG_8: return "MSG_8" ; default : return "MSG_UNKNOWN" } }
这段代码无论从可读性来说,还是从可维护性来说都是可以接收的。因此,当因为”高”复杂度就进行重构的话(例如:技巧2或技巧6),在降低圈复杂度的同时会带来不必要的逻辑复杂度。
当然,如果出现下面的情况的话,还是有必要进一步降低圈复杂度的:
消息数过多。
switch…case…多处重复。 对于消息过多的情况,可以考虑将消息进行分类,然后采用技巧1进行重构。对于出现多处重复的情况,可以通过技巧6将同样case的内容内聚到一个具体的类的方法中,然后通过多态的方式来使用。
例如下面两个代码片段的圈复杂度都是6。 代码片段1:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 string getWeight (int i) if (i <= 0 ) { return "no weight" ; } if (i < 10 ) { return "light" ; } if (i < 20 ) { return "medium" ; } if (i < 30 ) { return "heavy" ; } if (i < 40 ) { return "very heavy" ; } return "super heavy" }
代码片段2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 int sumOfNonPrimes (int limit) bool bAdd = false ; int sum = 0 ; for (int i = 0 ; i < limit; ++i) { if (i <= 2 ) continue ; for (int j = 2 ; j < i; ++j) { if (i % j == 0 ) { bAdd = false ; break ; } bAdd = true ; } if (bAdd) sum += i; } return sum; }
但是它们的代码无论从可读性上来说,还是从可维护性来说,代码片段1应该都优于代码片段2,代码片段2的坏味道更加浓郁。因此,圈复杂度还需要具体情况具体分析,其只能作为重构的一个度量指标,作为决策的一个参考依据。
圈复杂度的工具有很多,大致有三类:
类型
名称
说明
专用工具(单语言)
OCLint
C语言相关
GMetrics
Java
PyMetrics
python
JSComplexity
js
通用工具(多语言)
lizard
支持多种语言:C/C++ (works with C++14)、Java、C#、JavaScript、Objective C、Swift、Python、Ruby、PHP、Scala等。
sourcemonitor
免费、Windows平台。支持语言包括C、C++、C#、Java、VB、Delphi和HTML。
通用平台
sonarqube
一个用于代码质量管理的开源平台,支持20多种语言。通过插件机制可集成不同的测试工具,代码分析工具及持续集成工具
循環複雜度- 维基百科,自由的百科全书 Learn Mccabe’s Cyclomatic Complexity with Example McCabe’s Cyclomatic Complexity and Why We Don’t Use It